ليست مبالغة عندما يقال أن العلوم الرياضية والاحصائية هي لغة الكون!!!
الدافع للكتابة عن هذا الموضوع أن هذه الأيام أذاكر لبنتي - الله يحفظها- مادة الاحصاء الحيوي biostatistics كمتطلب عام لطلبة سنة أولى طب وتحديدا التوزيعات الاحتمالية probability distribution
ومحاولتي إقناعها بأهميتها في الواقع العملي بالأمثلة وتحفيزها لفهمها وإدراك مفهوم تلك التوزيعات وليس مجرد دراستها لتعدية تلك المادة كمتطلب جامعي فقط (لأنها تقول لي وش بستفيد منها في الطب وهنا ألقي العتب واللوم على أستاذة المادة لأني سألتها بتعجب…ليش المحاضرة ما شرحت لكم أهميتها في مجالكم وين ممكن تستفيدوا منها وتطبقوها … للأسف الإجابة …لا!!!)
عشان كذا قلت أشاركم توضيح لتلك التوزيعات وقد يكون هناك حالات شبيهة لحالة بنتي قد تستفيد من هذا الموضوع…
خلونا نرجع لمقولة ( العلوم الرياضية والاحصائية هي لغة الكون)!
خلونا نشوف توضيح هذا الادعاء ببعض الأمثلة ومن ثم احكموا بأنفسكم على ذلك!! قد تتفقون وقد يكون لكم وجهة نظر أخرى!
بداية لابد لنا أن نعلم أن الأنماط الممثلة للظواهر في الطبيعة تعيد وتكرر نفسها ( زي ما يقولون الواقع يعيد نفسه) مما يجعل بناء النماذج الرياضية والاحصائية ( التوزيعات الاحتمالية) لها ممكنة.
وفيما يلي عرض لبعض التوزيعات الاحتمالية الشائعة ومكان حدوثها بشكل طبيعي في الواقع الذي نعيشه…
التوزيع الطبيعي normal distribution - يشبه شكل الجرس 🛎️ وسمي طبيعي لأن معظم الظواهر في الطبيعة ( أوزان الناس، اطوالهم، معدلات ذكائهم،…) تتبع التوزيع الطبيعي.
أمثلة:
•أطوال الشبان: عندما تسأل 10000 من الشبان عن طولهم تجد أن أطوالهم تتوزع بين 150 إلى 110 سنتيميتر وبمتوسط 72 سنتيمتر. معظم الشبان تجدهم حول الذروة 72 سنتيمتر. وأما الاعداد الصغيرة جدا للطول تجدها عند 150 سنتيميتر و 110 سنتيمتر،
•كذلك توزيع انجاب الأطفال : تجد أن متوسط عدد الأطفال في الأسرة 3 (قمة التوزيع الطبيعي ) ،وإلى أقصى اليمين تجد عدد العائلات التي أنجبت 12 طفلا ، وإلى أقصى اليسار العائلة التي أنجبت طفلا واحدا أو لم تـُنجب.
يعتبر التوزيع أكثر التوزيعات الاحتمالية شهرة وقد اكتسب هذه الشهرة من نظرية النهاية المركزية وكونه أساسيا في الاحصاء الاستدلالي ( اختبارات الفرضيات)
توزيع بواسون Poisson distribution يصف احتمالية حدوث عدد معين من الأحداث في فترة زمنية أو مكانية محددة. يجب أن تحدث الأحداث بمعدل متوسط ثابت معروف ومستقلة عن بعضها البعض. وغالبا يستخدم توزيع پويسون للتنبؤ بالأحداث النادرة.
يمثل توزيع بواسون عدد مرات اضمحلال الذرة المشعة في فترة زمنية معينة، أو عدد السيارات التي تمر عبر نقطة معينة في إطار زمني معين.
مثال: إذا شهد تقاطع معين مرور 10 سيارات في المتوسط في الدقيقة الواحدة، فيمكن لتوزيع پويسون تقدير احتمال مرور ١٢ سيارة في الدقيقة التالية.
مثال آخر ( لمحبي ⚽️ ):في كرة القدم حيث تكون الأهداف نادرة، يمكنك استخدام التوزيع لنمذجة عدد الأهداف التي سجلها كل فريق.
المثال الأكثر شهرة للتطبيق العملي توزيع بواسون.
في عام 1946، نشر الإحصائي البريطاني كلارك "تطبيق توزيع بواسون"، والذي كشف فيه عن تحليله لتوزيع ضربات القنابل الطائرة (صواريخ V-1 وV-2) في لندن خلال الحرب العالمية الثانية. . وقد تعرضت بعض المناطق للقصف أكثر من غيرها. رغب الجيش البريطاني في معرفة ما إذا كان الألمان يستهدفون هذه المناطق (تشير الضربات إلى دقة فنية كبيرة) أو ما إذا كان التوزيع بسبب الصدفة. إذا كانت الصواريخ في الواقع موجهة بشكل عشوائي فقط (داخل منطقة أكثر عمومية)، فيمكن للبريطانيين ببساطة تفريق المنشآت المهمة لتقليل احتمالية إصابتها.
بدأ كلارك بتقسيم المنطقة إلى آلاف من قطع الأراضي الصغيرة والمتساوية الحجم. وفي كل من هذه، كان من غير المرجح أن تكون هناك ولو ضربة واحدة. علاوة على ذلك، وبافتراض أن الصواريخ سقطت بشكل عشوائي، فإن احتمال الإصابة في أي قطعة أرض واحدة سيكون ثابتًا في جميع القطع. لذلك، فإن العدد الإجمالي للنتائج سيكون مشابهًا إلى حد كبير لعدد الانتصارات في عدد كبير من التكرارات في لعبة الحظ مع احتمال ضئيل جدًا للفوز. قاد هذا النوع من التفكير كلارك إلى الاشتقاق الرسمي لتوزيع بواسون كنموذج. كانت تكرارات الضربة المرصودة قريبة جدًا من تكرارات بواسون المتوقعة. ومن ثم، ذكر كلارك أن الاختلافات المرصودة يبدو أنها نشأت عن طريق الصدفة فقط.
…تابع
الدافع للكتابة عن هذا الموضوع أن هذه الأيام أذاكر لبنتي - الله يحفظها- مادة الاحصاء الحيوي biostatistics كمتطلب عام لطلبة سنة أولى طب وتحديدا التوزيعات الاحتمالية probability distribution
ومحاولتي إقناعها بأهميتها في الواقع العملي بالأمثلة وتحفيزها لفهمها وإدراك مفهوم تلك التوزيعات وليس مجرد دراستها لتعدية تلك المادة كمتطلب جامعي فقط (لأنها تقول لي وش بستفيد منها في الطب وهنا ألقي العتب واللوم على أستاذة المادة لأني سألتها بتعجب…ليش المحاضرة ما شرحت لكم أهميتها في مجالكم وين ممكن تستفيدوا منها وتطبقوها … للأسف الإجابة …لا!!!)
عشان كذا قلت أشاركم توضيح لتلك التوزيعات وقد يكون هناك حالات شبيهة لحالة بنتي قد تستفيد من هذا الموضوع…
خلونا نرجع لمقولة ( العلوم الرياضية والاحصائية هي لغة الكون)!
خلونا نشوف توضيح هذا الادعاء ببعض الأمثلة ومن ثم احكموا بأنفسكم على ذلك!! قد تتفقون وقد يكون لكم وجهة نظر أخرى!
بداية لابد لنا أن نعلم أن الأنماط الممثلة للظواهر في الطبيعة تعيد وتكرر نفسها ( زي ما يقولون الواقع يعيد نفسه) مما يجعل بناء النماذج الرياضية والاحصائية ( التوزيعات الاحتمالية) لها ممكنة.
وفيما يلي عرض لبعض التوزيعات الاحتمالية الشائعة ومكان حدوثها بشكل طبيعي في الواقع الذي نعيشه…
التوزيع الطبيعي normal distribution - يشبه شكل الجرس 🛎️ وسمي طبيعي لأن معظم الظواهر في الطبيعة ( أوزان الناس، اطوالهم، معدلات ذكائهم،…) تتبع التوزيع الطبيعي.
أمثلة:
•أطوال الشبان: عندما تسأل 10000 من الشبان عن طولهم تجد أن أطوالهم تتوزع بين 150 إلى 110 سنتيميتر وبمتوسط 72 سنتيمتر. معظم الشبان تجدهم حول الذروة 72 سنتيمتر. وأما الاعداد الصغيرة جدا للطول تجدها عند 150 سنتيميتر و 110 سنتيمتر،
•كذلك توزيع انجاب الأطفال : تجد أن متوسط عدد الأطفال في الأسرة 3 (قمة التوزيع الطبيعي ) ،وإلى أقصى اليمين تجد عدد العائلات التي أنجبت 12 طفلا ، وإلى أقصى اليسار العائلة التي أنجبت طفلا واحدا أو لم تـُنجب.
يعتبر التوزيع أكثر التوزيعات الاحتمالية شهرة وقد اكتسب هذه الشهرة من نظرية النهاية المركزية وكونه أساسيا في الاحصاء الاستدلالي ( اختبارات الفرضيات)
توزيع بواسون Poisson distribution يصف احتمالية حدوث عدد معين من الأحداث في فترة زمنية أو مكانية محددة. يجب أن تحدث الأحداث بمعدل متوسط ثابت معروف ومستقلة عن بعضها البعض. وغالبا يستخدم توزيع پويسون للتنبؤ بالأحداث النادرة.
يمثل توزيع بواسون عدد مرات اضمحلال الذرة المشعة في فترة زمنية معينة، أو عدد السيارات التي تمر عبر نقطة معينة في إطار زمني معين.
مثال: إذا شهد تقاطع معين مرور 10 سيارات في المتوسط في الدقيقة الواحدة، فيمكن لتوزيع پويسون تقدير احتمال مرور ١٢ سيارة في الدقيقة التالية.
مثال آخر ( لمحبي ⚽️ ):في كرة القدم حيث تكون الأهداف نادرة، يمكنك استخدام التوزيع لنمذجة عدد الأهداف التي سجلها كل فريق.
المثال الأكثر شهرة للتطبيق العملي توزيع بواسون.
في عام 1946، نشر الإحصائي البريطاني كلارك "تطبيق توزيع بواسون"، والذي كشف فيه عن تحليله لتوزيع ضربات القنابل الطائرة (صواريخ V-1 وV-2) في لندن خلال الحرب العالمية الثانية. . وقد تعرضت بعض المناطق للقصف أكثر من غيرها. رغب الجيش البريطاني في معرفة ما إذا كان الألمان يستهدفون هذه المناطق (تشير الضربات إلى دقة فنية كبيرة) أو ما إذا كان التوزيع بسبب الصدفة. إذا كانت الصواريخ في الواقع موجهة بشكل عشوائي فقط (داخل منطقة أكثر عمومية)، فيمكن للبريطانيين ببساطة تفريق المنشآت المهمة لتقليل احتمالية إصابتها.
بدأ كلارك بتقسيم المنطقة إلى آلاف من قطع الأراضي الصغيرة والمتساوية الحجم. وفي كل من هذه، كان من غير المرجح أن تكون هناك ولو ضربة واحدة. علاوة على ذلك، وبافتراض أن الصواريخ سقطت بشكل عشوائي، فإن احتمال الإصابة في أي قطعة أرض واحدة سيكون ثابتًا في جميع القطع. لذلك، فإن العدد الإجمالي للنتائج سيكون مشابهًا إلى حد كبير لعدد الانتصارات في عدد كبير من التكرارات في لعبة الحظ مع احتمال ضئيل جدًا للفوز. قاد هذا النوع من التفكير كلارك إلى الاشتقاق الرسمي لتوزيع بواسون كنموذج. كانت تكرارات الضربة المرصودة قريبة جدًا من تكرارات بواسون المتوقعة. ومن ثم، ذكر كلارك أن الاختلافات المرصودة يبدو أنها نشأت عن طريق الصدفة فقط.
…تابع
التوزيع ذو الحدين Binomial distribution يصف عدد النجاحات في عدد محدد من التجارب ( نجاح/فشل) المستقلة، ولكل منها نفس احتمالية النجاح.
على سبيل المثال، يمكن تمثيل عدد الصور عند رمي عملة معدنية عدة مرات، أو عدد العناصر المعيبة في مجموعة من السلع المصنعة أو عدد الأفراد الذي صوتوا بالتأييد في استطلاع رأي حول قضية ما باستخدام هذا التوزيع.
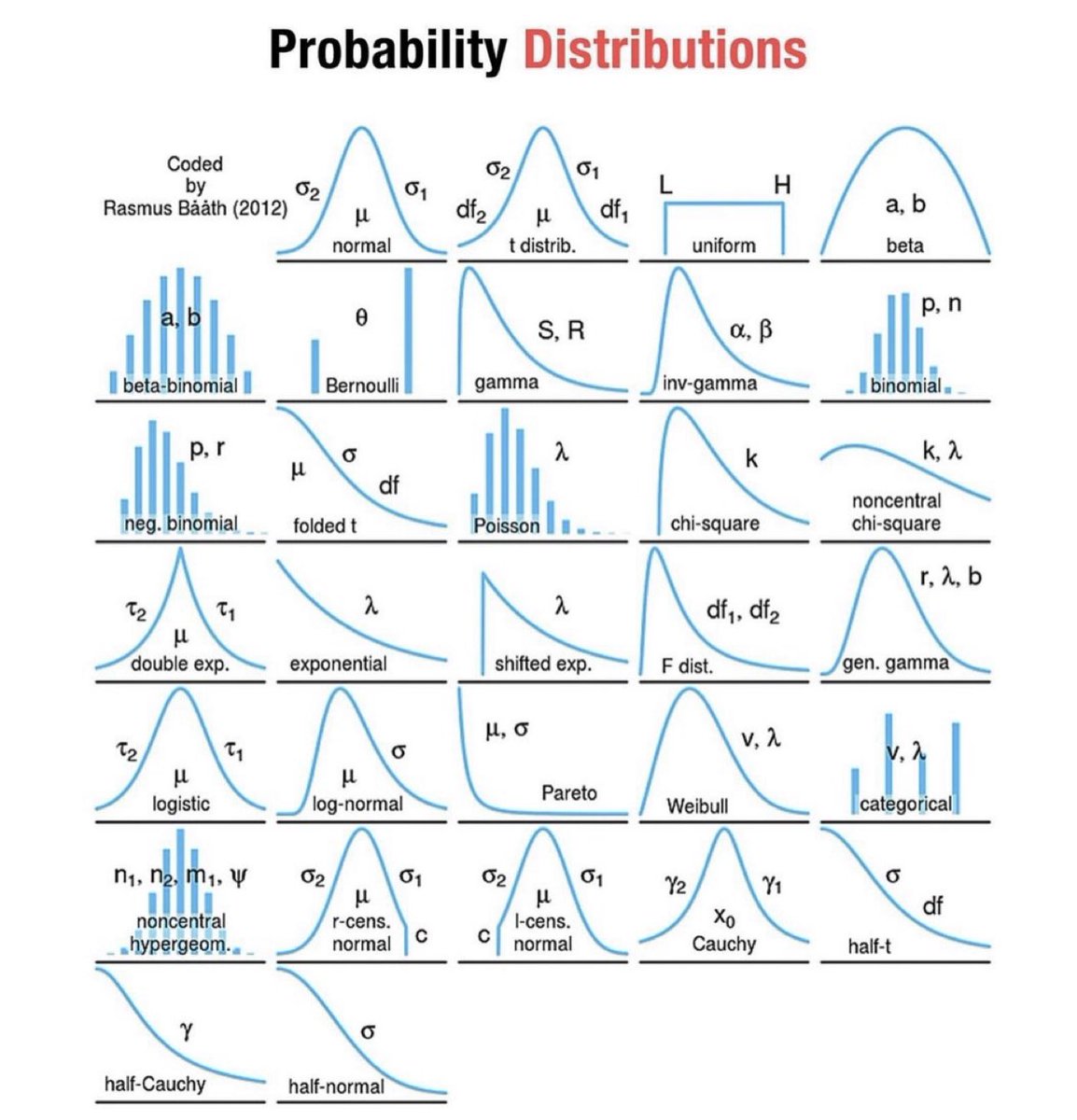
هذا ملخص للتوزيعات الأكثر شيوعا، والشكل أدناه بوجد به حصر لمجموعة من التوزيعات الاحتمالية الأخرى…تتحدث هذه التوزيعات التي تحدث بشكل طبيعي عن سبب كون النماذج الاحصائية والرياضية لغة الكون وكيف يمكنك استخدامها لنمذجة سلوكه والتنبؤ به
على سبيل المثال، يمكن تمثيل عدد الصور عند رمي عملة معدنية عدة مرات، أو عدد العناصر المعيبة في مجموعة من السلع المصنعة أو عدد الأفراد الذي صوتوا بالتأييد في استطلاع رأي حول قضية ما باستخدام هذا التوزيع.
هذا ملخص للتوزيعات الأكثر شيوعا، والشكل أدناه بوجد به حصر لمجموعة من التوزيعات الاحتمالية الأخرى…تتحدث هذه التوزيعات التي تحدث بشكل طبيعي عن سبب كون النماذج الاحصائية والرياضية لغة الكون وكيف يمكنك استخدامها لنمذجة سلوكه والتنبؤ به
جاري تحميل الاقتراحات...