🔸حكاية لتبسيط مفهوم إختبار النظرية Hypothesis testing #البحث_العلمي 🧵
في إحدى قاعات المحاكم هناك شاب في متوسط العمر يواجه تهمة سرقة بنك ، ويقوم ممثل الإدعاء العام بمحاولة إيجاد الدليل لإدانته، بينما يستمع اعضاء هيئة المحلفين للمحاكمة للتداول واعطاء الحكم
في إحدى قاعات المحاكم هناك شاب في متوسط العمر يواجه تهمة سرقة بنك ، ويقوم ممثل الإدعاء العام بمحاولة إيجاد الدليل لإدانته، بينما يستمع اعضاء هيئة المحلفين للمحاكمة للتداول واعطاء الحكم
قاعدة معروفة: المتهم برئ حتى تثبت إدانته/ الفرضية الصفرية
المتهم يقوم مقام السؤال البحثي
المدعي العام هو الباحث
القاضي هو نتائج البحث
يقول المدعي العام (الباحث)بما انه المتهم برئ للآن سيكون هناك احتمال ضعيف ان نجد دليل إدانه ولكننا ان وجدناه فسيكون المتهم غير برئ (مذنب)
المتهم يقوم مقام السؤال البحثي
المدعي العام هو الباحث
القاضي هو نتائج البحث
يقول المدعي العام (الباحث)بما انه المتهم برئ للآن سيكون هناك احتمال ضعيف ان نجد دليل إدانه ولكننا ان وجدناه فسيكون المتهم غير برئ (مذنب)
الاحتمال الضعيف هذا قدرناه ب 5%
وهذي نسبة ألفا type I erorr
الآن هناك أربعة احتمالات لما سيحصل بعد دراسة الأدلة: ٢جيدة ، ٢ سيئة
الجيدة:
١.القاضي سيحكم بان المتهم برئ ويطلعه وهو فعلًا برئ وهنا القاضي لم ينقض الفرضية الصفرية- ممتاز
وهذي نسبة ألفا type I erorr
الآن هناك أربعة احتمالات لما سيحصل بعد دراسة الأدلة: ٢جيدة ، ٢ سيئة
الجيدة:
١.القاضي سيحكم بان المتهم برئ ويطلعه وهو فعلًا برئ وهنا القاضي لم ينقض الفرضية الصفرية- ممتاز
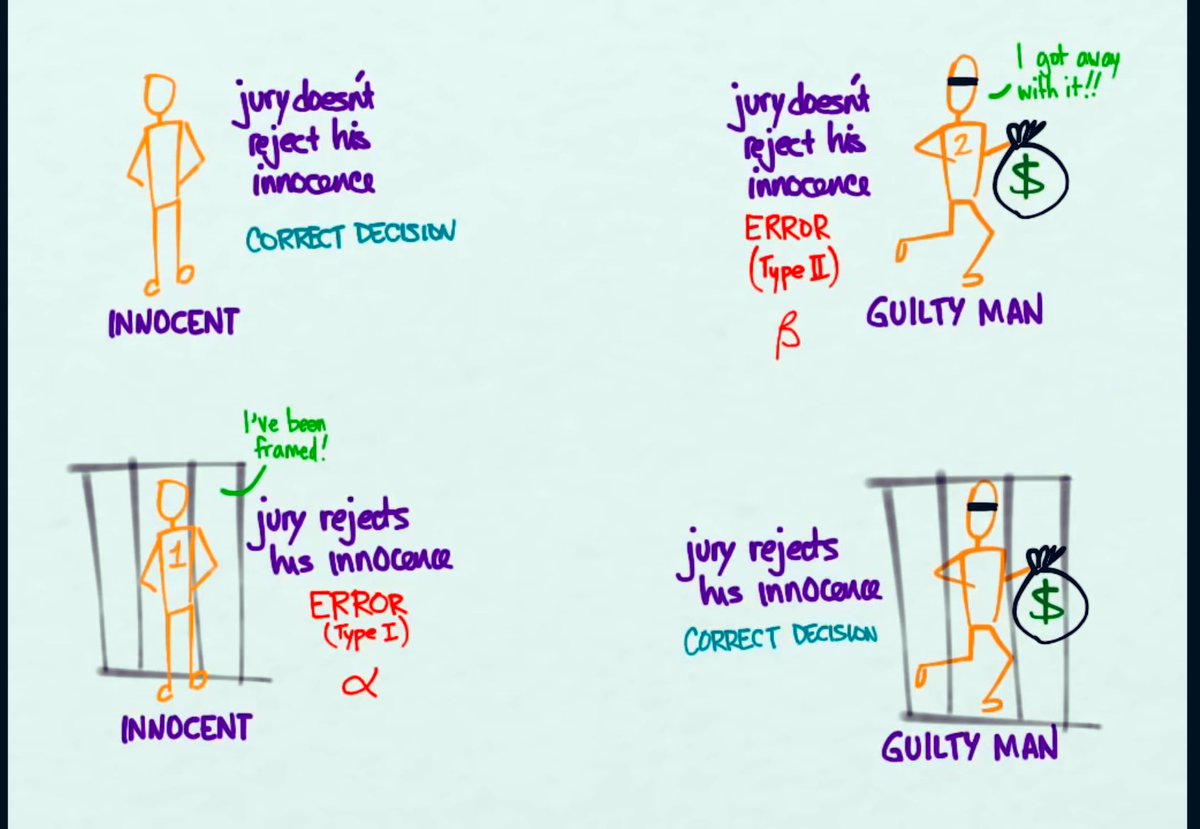
٢.القاضي سيحكم انه مذنب (سينقض الفرضية الصفرية) وهو فعلًا مذنب - ممتاز
السيئة:
١.القاضي سيحكم بأنه مذنب ويحبسه ولكنه في الحقيقة برئ ، هذا الخطأ هو Type I error ألفا فهو رفض الفرضية الصفرية لوجود الدليل مثل ما قال المدعي العام بالبداية
السيئة:
١.القاضي سيحكم بأنه مذنب ويحبسه ولكنه في الحقيقة برئ ، هذا الخطأ هو Type I error ألفا فهو رفض الفرضية الصفرية لوجود الدليل مثل ما قال المدعي العام بالبداية
تذكر لا احد يعرف الحقيقة الا المتهم نفسه ولكن ليس لدينا حل الا اتباع الأدله، العواقب هنا حبس شخص برئ ، لذلك يقال انه مذنب حسب الأدله
وفي الأبحاث نقول we reject the null hypothesis
وفي الأبحاث نقول we reject the null hypothesis
٢.القاضي سيحكم بأن المتهم برئ ويطلعه ولكن في الحقيقة هو مذنب ، هذا الخطأ هو Type II error بيتا وهنا القاضي لم يجد دليل كافي لإدانته برغم احساسه انه مذنب.
لذلك يقال في الأبحاث we failed to reject the null hypothesis
لذلك يقال في الأبحاث we failed to reject the null hypothesis
بين الخطئين الاول والثاني ،الأول يعتبر أخطر ومؤلم او مكلف اكثر فتكون نسبته اقل
Type I erorr is 5% Alph
Type II erorr is 20% Beta
القاضي هنا هو نتائج التحليل الإحصائي التي لها الحكم. الفرق انه القاضي غالبا لا يتأثر بالتحيزات بعكس التحليل الإحصائي يتأثر بجودة البيانات و bias
Type I erorr is 5% Alph
Type II erorr is 20% Beta
القاضي هنا هو نتائج التحليل الإحصائي التي لها الحكم. الفرق انه القاضي غالبا لا يتأثر بالتحيزات بعكس التحليل الإحصائي يتأثر بجودة البيانات و bias
وشكرا @rattibha
من أجواء مسلسل suits 😃
من أجواء مسلسل suits 😃
جاري تحميل الاقتراحات...