في الإحصاء وتحليل البيانات الحصول على نتائج مهمة سهلة،بيانات وتطبق خوارزمية عليها.المهم هو فهم البيانات ثم تفسير النتائج
أسئلة بسيطة مثل لماذا استخدم المتوسط وليس الوسيط أو العكس؟
ما فائدة التباين والانحراف المعياري؟
سأحاول شرح هذه المفاهيم وماذا تفيد محلل بيانات
#علم_البيانات
أسئلة بسيطة مثل لماذا استخدم المتوسط وليس الوسيط أو العكس؟
ما فائدة التباين والانحراف المعياري؟
سأحاول شرح هذه المفاهيم وماذا تفيد محلل بيانات
#علم_البيانات
بعد جمع البيانات بغرض تحليلها لأي هدف. تكون أول مهمة هي استكشاف البيانات data exploration وهذه تحتوي على عدة خطوات من ضمنها معرفة مركزية البيانات وتوزيع البيانات وغيرها
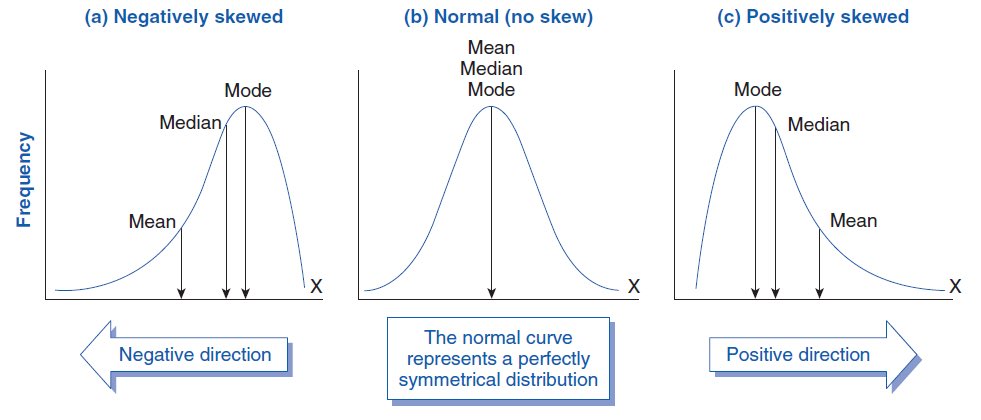
من مقاييس central tendency المتوسط mean و الوسيط median
من مقاييس central tendency المتوسط mean و الوسيط median
لنفترض عندنا هذه العينة
2, 5, 6, 7, 8, 13, 14,16, 91
المتوسط هو مجموعها على عددها ويكون ١٦٢ / ٩ والناتج ١٨
والوسيط هو منتصف الارقام بعد ترتيبها تصاعدياً (الخانة رقم ٥) وهو ٨
لو كنا بنحسب متوسط الرواتب فهل هو ١٨ الف أو ٨ آلاف
هنا المعلومة تفرق كثير
2, 5, 6, 7, 8, 13, 14,16, 91
المتوسط هو مجموعها على عددها ويكون ١٦٢ / ٩ والناتج ١٨
والوسيط هو منتصف الارقام بعد ترتيبها تصاعدياً (الخانة رقم ٥) وهو ٨
لو كنا بنحسب متوسط الرواتب فهل هو ١٨ الف أو ٨ آلاف
هنا المعلومة تفرق كثير
طبعاً السبب لهذا الفرق هو القيمة الشاذة ٩١. لذلك المتوسط يتأثر بالقيم الشاذة (ممكن نحذفها)
لكن أحياناً نحتاج بقاء القيم الشاذة. القيم الشاذة هي دليل الاحتيال في تحليل credit card أيضا حساب متوسط درجات طلاب في مادة هنا لابد أن نأخذ كل القيم.
لكن أحياناً نحتاج بقاء القيم الشاذة. القيم الشاذة هي دليل الاحتيال في تحليل credit card أيضا حساب متوسط درجات طلاب في مادة هنا لابد أن نأخذ كل القيم.
فالخلاصة بين اختيار المتوسط أو الوسيط هو أننا نحتاج نشوف التوزيع
إذا كان طبيعي normal نختار المتوسط
إذا فيه انحراف skewed نختار الوسيط
كما في الصورة
إذا كان طبيعي normal نختار المتوسط
إذا فيه انحراف skewed نختار الوسيط
كما في الصورة
ممكن نختبر ال normality للبيانات السابقة من خلال هذا الموقع (طبعاً بدون الدخول في أنواع اختبار ال normality)
statskingdom.com
statskingdom.com
بتكون النتيجة
statskingdom.com
statskingdom.com
بتكون النتيجة
الآن نشوف التباين variance والانحراف المعياري standard deviation
تعتبر من مقاييس التشتت dispersion
وتقيس مدى انتشار أو تباعد النقاط عن بعضها أو عن متوسطها
نأخذ مثال لمعرفة لماذا نحتاج هذه المقاييس
تعتبر من مقاييس التشتت dispersion
وتقيس مدى انتشار أو تباعد النقاط عن بعضها أو عن متوسطها
نأخذ مثال لمعرفة لماذا نحتاج هذه المقاييس
لنفرض لدينا عينتين
48,49,50,51,52
و
10,30,50,70,90
المتوسط لكل العينتين هو ٥٠
هنا نحتاج لمقياس أخر للتفريق أو مقارنة العينتين.
لذلك الانحراف المعياري للعينة الأولى: ١.٥٨
وللثانية: ٣١.٦٢
يوجد فرق لكن ماذا يعني هذا؟
48,49,50,51,52
و
10,30,50,70,90
المتوسط لكل العينتين هو ٥٠
هنا نحتاج لمقياس أخر للتفريق أو مقارنة العينتين.
لذلك الانحراف المعياري للعينة الأولى: ١.٥٨
وللثانية: ٣١.٦٢
يوجد فرق لكن ماذا يعني هذا؟
يعني أن العينة الأولى منتشرة بشكل متقارب حول المتوسط أي أن القيم قريبة من بعض ومن متوسطها
والعينة الثانية القيم متباعدة.
حتى نفهم لنفرض أن لدينا بيانات الأجور لشركة A حيث أن متوسط الرواتب ٢٠ الف والانحراف المعياري ١٥ الف.
وشركة B متوسط الأجور ٢٠ الف والانحراف المعياري ٢٠٠٠
والعينة الثانية القيم متباعدة.
حتى نفهم لنفرض أن لدينا بيانات الأجور لشركة A حيث أن متوسط الرواتب ٢٠ الف والانحراف المعياري ١٥ الف.
وشركة B متوسط الأجور ٢٠ الف والانحراف المعياري ٢٠٠٠
نفهم من هذا أن رواتب الشركة A بينها تفاوت كبير. فيه موظف ممكن يأخذ ٣٥ الف وأخر يأخذ ٥ الاف
على عكس رواتب شركة B متقاربة أكثر
طبعا هذا مثال لتوضيح
ولو قسنا على تقييم فصلين دراسيين بيكون الفصل B مستواهم متقارب أكثر من A
نشوف تعريف التباين والانحراف وإن شاء الله تكون الصورة أوضح
على عكس رواتب شركة B متقاربة أكثر
طبعا هذا مثال لتوضيح
ولو قسنا على تقييم فصلين دراسيين بيكون الفصل B مستواهم متقارب أكثر من A
نشوف تعريف التباين والانحراف وإن شاء الله تكون الصورة أوضح
التباين variance هو متوسط الانحراف التربيعي لمتغيرات عشوائية عن متوسط العينة sample أو متوسط ال population
كما في الصورة المتغير العشوائي هو مثلاً أول طول ١٧٣
ومتوسط population وهو ١٥٥
يكون الانحراف هو الفوق ١٧٣-١٥٥ ويساوي ١٨
كما في الصورة المتغير العشوائي هو مثلاً أول طول ١٧٣
ومتوسط population وهو ١٥٥
يكون الانحراف هو الفوق ١٧٣-١٥٥ ويساوي ١٨
نحتاج التربيع square لوجود قيم سالبة مثلاً ثاني طول من اليسار هو ١٤٧ ويكون الفرق عن المتوسط ١٤٧ - ١٥٥ هو -٨
لذا نحتاج التربيع للتخلص من القيم السالبة
لذا نحتاج التربيع للتخلص من القيم السالبة
عند تطبيق معادلة الانحراف لل population تكون القيمة ١٣٢.٣٣ لكن الوحدة هي cm^2 (تربيع)
هنا يصعب مقارنته مع الطول الموجود مثلاً ١٧٣ بسبب اختلاف الوحدة. لذلك نحتاج للانحراف المعياري
هنا يصعب مقارنته مع الطول الموجود مثلاً ١٧٣ بسبب اختلاف الوحدة. لذلك نحتاج للانحراف المعياري
الانحراف المعياري standard deviation
هو الجذر التربيعي square root للتباين
ويمكن حسابه مباشرة من المعادلة
ويكون في مثال الطول ١١.٥٠ والوحدة cm
هو الجذر التربيعي square root للتباين
ويمكن حسابه مباشرة من المعادلة
ويكون في مثال الطول ١١.٥٠ والوحدة cm
سؤال منطقي لماذا نحتاج الاثنين التباين والانحراف المعياري هل يكفي واحد منهم؟
أول فرق بينهم الانحراف المعياري له نفس وحدة القيم أو المتغيرات العشوائي ولكن التباين هو وحدة مربعة squared
أول فرق بينهم الانحراف المعياري له نفس وحدة القيم أو المتغيرات العشوائي ولكن التباين هو وحدة مربعة squared
أيضا الانحراف المعياري مناسب أكثر في التحليل الوصفي descriptive analysis بمعنى وصف مدى انتشار النقاط عن متوسطها الخ
التباين مناسب في حالات إذا كنا نريد مقارنة مجموعات مع بعض. تحديد في parametric tests من الافتراضات يكون للمجموعات نفس التباين ( ممكن نشرحه في موضوع مستقل)
التباين مناسب في حالات إذا كنا نريد مقارنة مجموعات مع بعض. تحديد في parametric tests من الافتراضات يكون للمجموعات نفس التباين ( ممكن نشرحه في موضوع مستقل)
سؤال بسيط بدون ما نبحث
إذا الانحراف المعياري كان صفر ماذا يعني؟
أيضا في معادلات الsample لماذا نقسم على n-1
إذا الانحراف المعياري كان صفر ماذا يعني؟
أيضا في معادلات الsample لماذا نقسم على n-1
في هذه السلسلة حاولت توضيح بعض الأساسيات بشكل عام وأيضا نحتاجها في شرح التباين في الانحدار regression
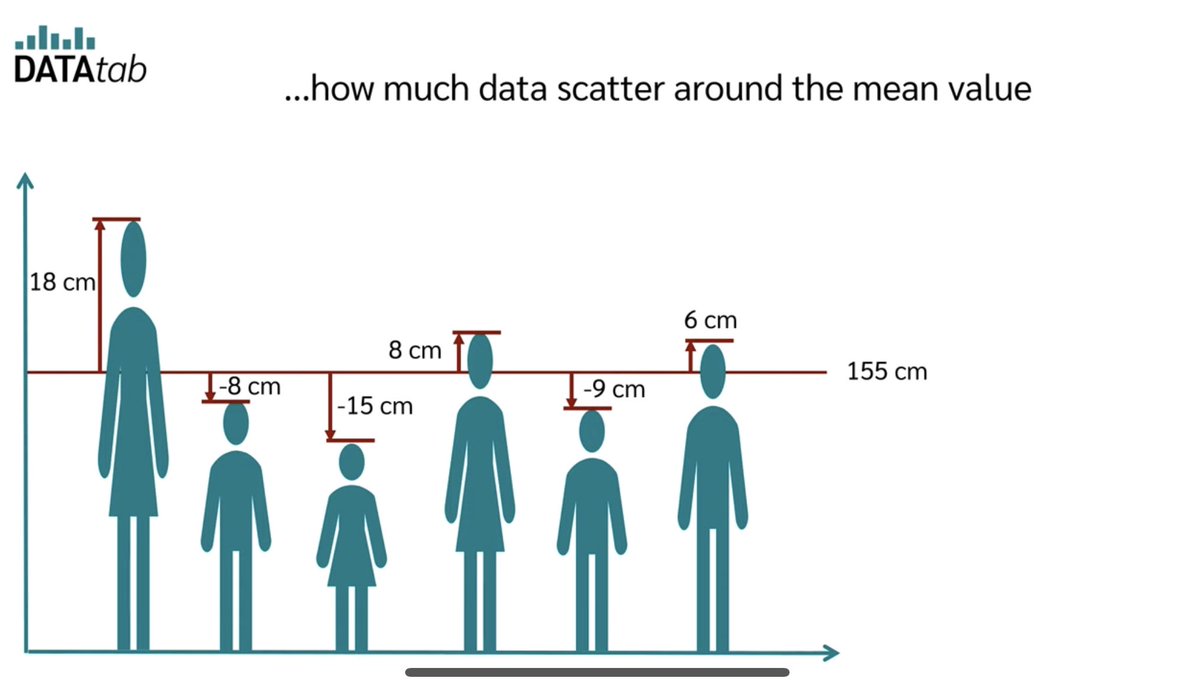
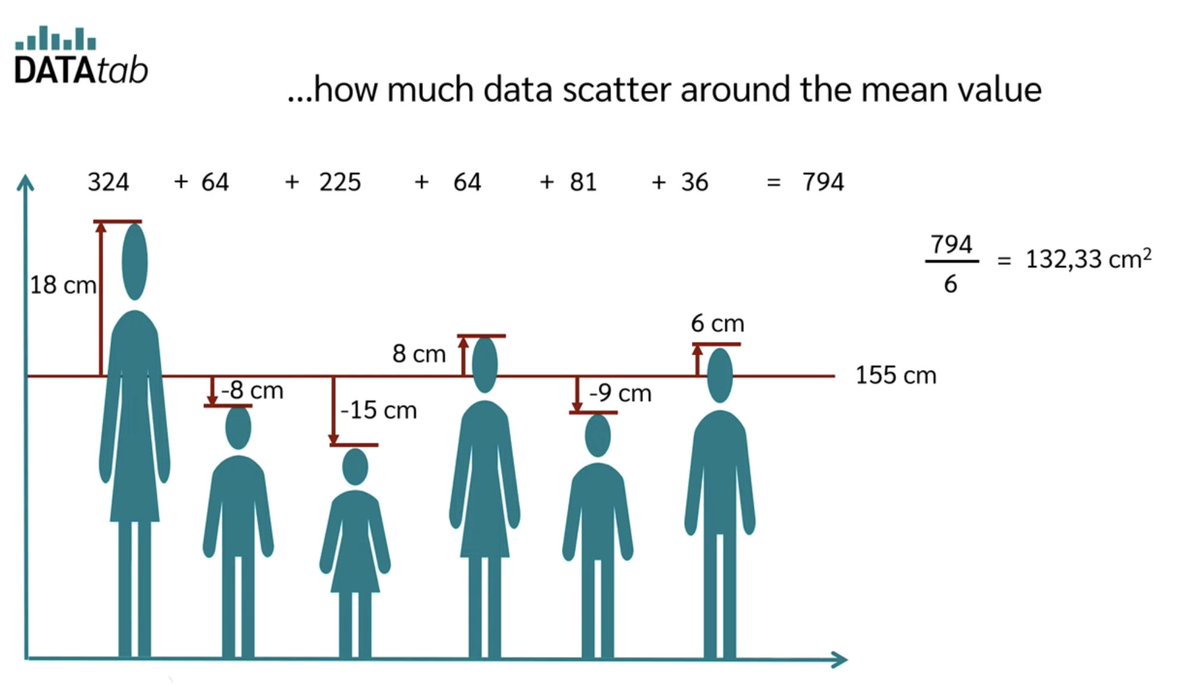
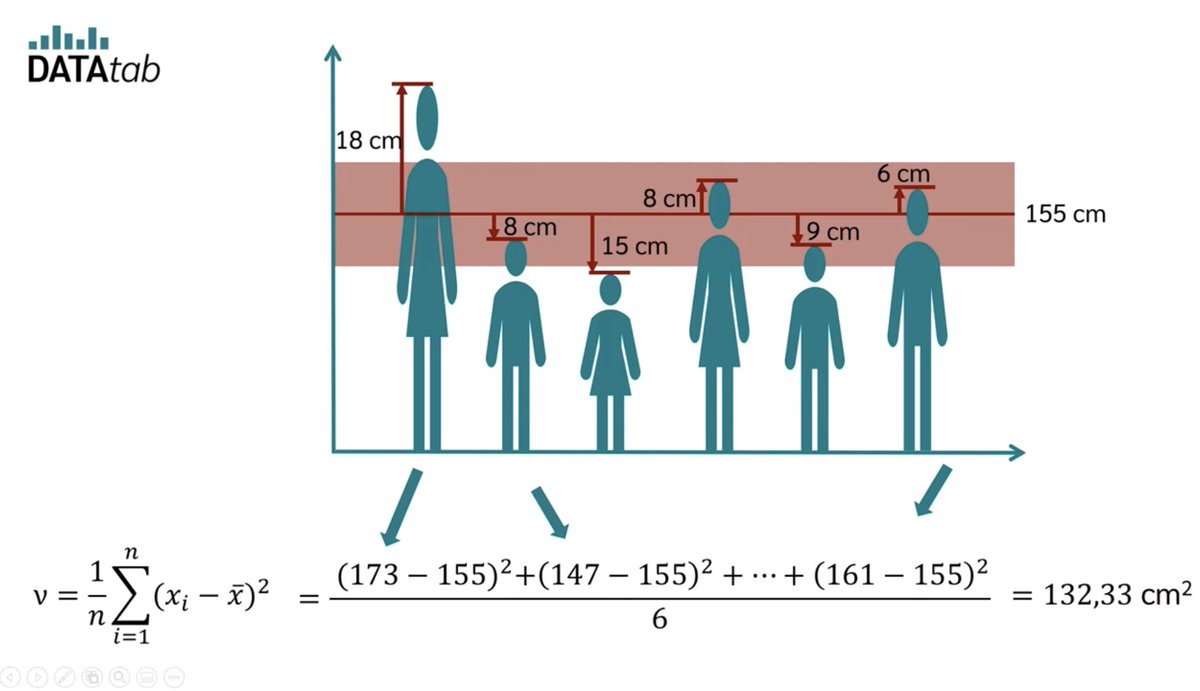
أخيراً: صور مثال الطول من هذا المقطع
youtu.be
أخيراً: صور مثال الطول من هذا المقطع
youtu.be
جاري تحميل الاقتراحات...