لغز Monty Hall
واحدة من أكثر نظريات الرياضيات اللي أثارت الجدل، لكن اختبارها مرارا و تكرارا أثبت جدواها
أنت في برنامج ألعاب تلفزيوني، و يطلب منك المقدم اختيار باب واحد من أصل ٣:
باب واحد وراه سيارة، و البابين الباقيين وراهم خرفان.. أنت بطبيعة الحال تبي تختار السيارة
واحدة من أكثر نظريات الرياضيات اللي أثارت الجدل، لكن اختبارها مرارا و تكرارا أثبت جدواها
أنت في برنامج ألعاب تلفزيوني، و يطلب منك المقدم اختيار باب واحد من أصل ٣:
باب واحد وراه سيارة، و البابين الباقيين وراهم خرفان.. أنت بطبيعة الحال تبي تختار السيارة
يطلب منك المقدم اختيار باب، علما أنه يعلم ما هو موجود خلف كل واحد، فتختار الباب رقم ١
و عندك احتمالية 1/3 أن يكون اختيارك صحيح لأن كل باب له احتمالية أن يكون صحيح بنسبة 1/3
يقوم المقدم بفتح الباب رقم ٣، و يطلع وراه خروف
و عندك احتمالية 1/3 أن يكون اختيارك صحيح لأن كل باب له احتمالية أن يكون صحيح بنسبة 1/3
يقوم المقدم بفتح الباب رقم ٣، و يطلع وراه خروف
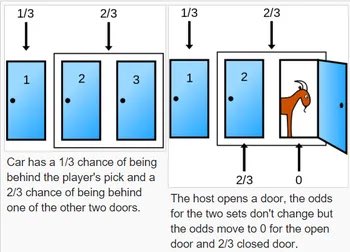
بعد فتح الباب الثالث، شو احتمالية أن يكون الباب الأول هو اللي وراه سيارة؟
الجواب هو 33.3%
بتقول كيف؟ من ٣ أبواب صاروا بابين.. ليش مب الاحتمالية صارت 50%؟
ببساطة لأن الباب اللي انت اخترته احتمالية صحته هي 1/3 أو 33.3%
بينما مجموع احتمالية ما لم تختاره أنت هو 66.7% موزعة على بابين.. لكن بعد خروج باب من الحسبة.. بقت هذه الاحتمالية عند الباب الثاني
بتقول كيف؟ من ٣ أبواب صاروا بابين.. ليش مب الاحتمالية صارت 50%؟
ببساطة لأن الباب اللي انت اخترته احتمالية صحته هي 1/3 أو 33.3%
بينما مجموع احتمالية ما لم تختاره أنت هو 66.7% موزعة على بابين.. لكن بعد خروج باب من الحسبة.. بقت هذه الاحتمالية عند الباب الثاني
و بالتالي لما يتم سؤالك إذا كنت ناوي تغير خيارك من الباب الأول إلى الباب الثاني، حسابيا أفضل لك دائما أن تختار الباب الثاني
أعطيك مثال آخر ممكن يفهمك بشكل أفضل.. افرض عندك 100 باب و ليس 3
99 منهم وراهم خرفان و واحد فيهم وراه سيارة
اخترت باب .. احتمالية صحة خيارك هي 1/100 أو 1% فقط
لو قام مقدم البرنامج بفتح 98 باب و كلهم وراهم خرفان.. تبقى بابين فقط
هل بتبقى على بابك و بإحتمالية 1%؟ أو بتحول؟
99 منهم وراهم خرفان و واحد فيهم وراه سيارة
اخترت باب .. احتمالية صحة خيارك هي 1/100 أو 1% فقط
لو قام مقدم البرنامج بفتح 98 باب و كلهم وراهم خرفان.. تبقى بابين فقط
هل بتبقى على بابك و بإحتمالية 1%؟ أو بتحول؟
لما يتم تكررارها على عدة مرات حسب ما قام به علماء الرياضيات لدراسة الاحتمالات، تبين صحة النظرية و هي أنه التغيير دائما أفضل لك في هالحالة
جاري تحميل الاقتراحات...