#خوارزميون
@PrograminLovers
مقدمة في أساسيات تصميم الخوارزميات – الخوارزميات الجشعة/الطماعة:
تستخدم الخوارزميات الجشعة عادة لحل مشاكل التحسين وهي المشاكل التي تهدف إلى تقليص أو زيادة كمية معينة.
@PrograminLovers
مقدمة في أساسيات تصميم الخوارزميات – الخوارزميات الجشعة/الطماعة:
تستخدم الخوارزميات الجشعة عادة لحل مشاكل التحسين وهي المشاكل التي تهدف إلى تقليص أو زيادة كمية معينة.
ومن أمثلتها: مشكلة ضغط البيانات التي تهدف إلى تقليص حجم البيانات إلى أقصى حد ممكن، ومشكلة الحقيبة التي تهدف تعبئة حقيبة بمجموعة من الأغراض بحيث تكون القيمة الإجمالية لهذه الأغراض أقصى ما يمكن.
وتنتهج الخوارزميات الجشعة التدرج في حل المشكلة من خلال سلسلة من الخطوات، بحيث تقوم كل خطوة بإضافة جزء من حل المشكلة على ما تم بناءه في الخطوات السابقة، حتى يتم الوصول إلى حل كامل للمشكلة.
ويجب أن تلبي كل خطوة في الخوارزمية الشروط التالية:
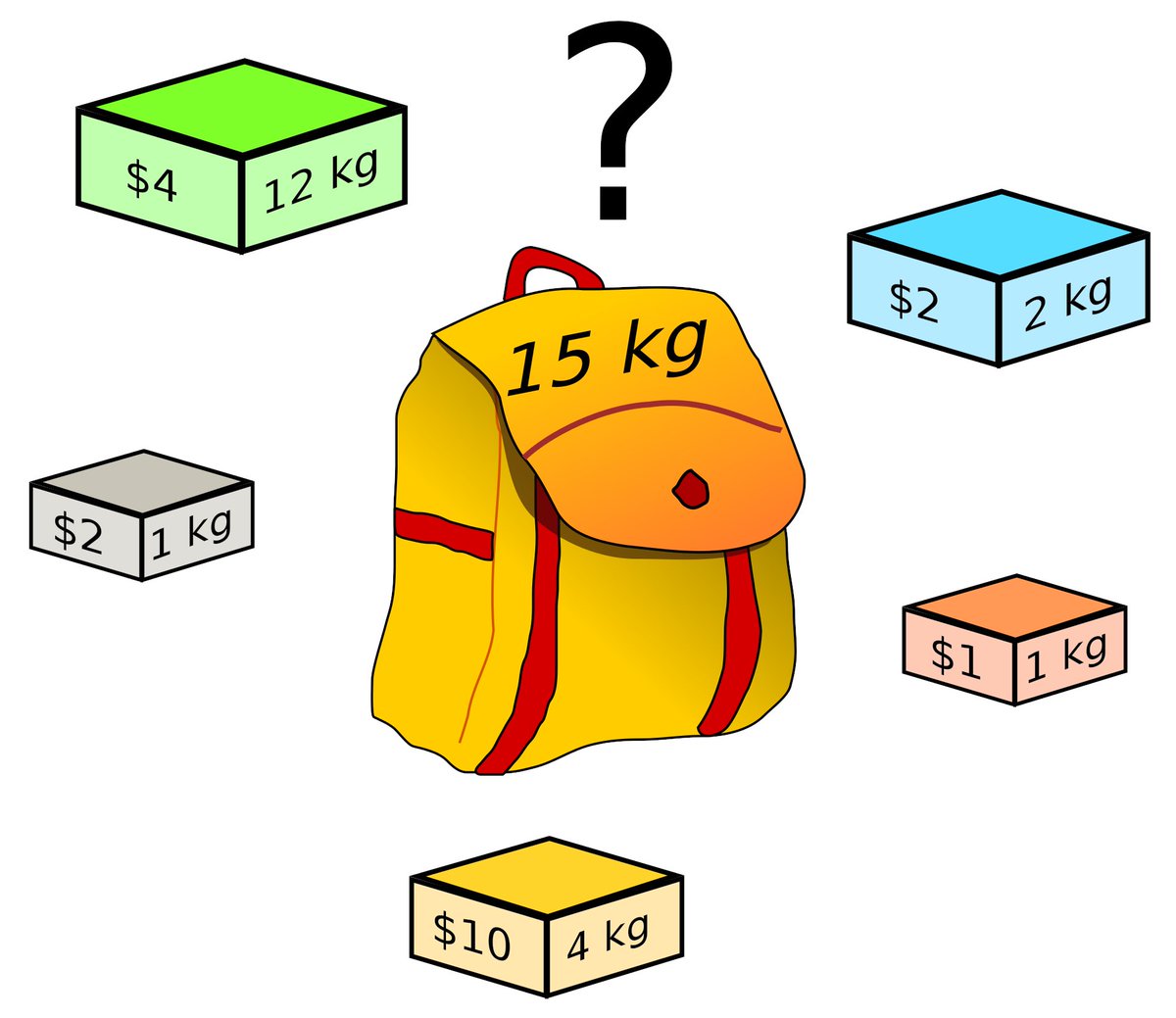
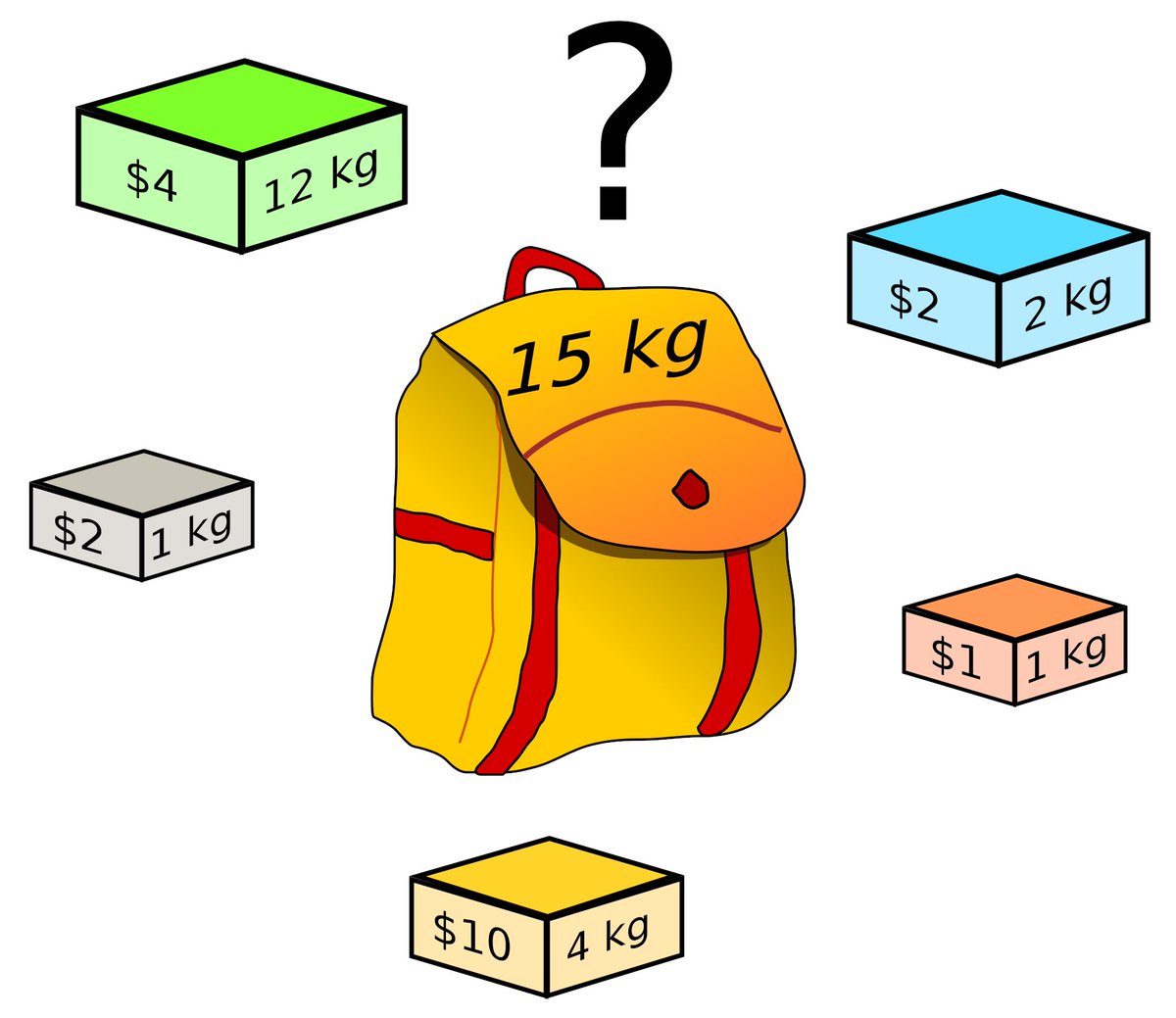
* أن يكون الحل الذي تم اختياره صحيحا ويلبي متطلبات المشكلة. مثلا في مشكلة الحقيبة لا يجب أن يتجاوز حجم الأغراض التي يتم اختيارها في كل خطوة حجم الحقيبة
* أن يكون الحل الذي تم اختياره صحيحا ويلبي متطلبات المشكلة. مثلا في مشكلة الحقيبة لا يجب أن يتجاوز حجم الأغراض التي يتم اختيارها في كل خطوة حجم الحقيبة
* أن يكون الحل الذي يتم اختياره هو أفضل الحلول المتاحة في هذه الخطوة. مثلا في مشكلة الحقيبة لا يمكن اختيار غرض من الأغراض المتبقية مع وجود غرض أعلى منه قيمة إذا كانت الحقيبة تتسع له.
* لا يجب أن تتسبب الخطوة الحالية في إلغاء أي من الخطوات السابقة أو التأثير سلبا على قيمة الحل الذي تم بناؤه. مثلا في مشكلة الحقيبة لا يمكن لأي خطوة أن تتخلص من الأغراض التي تم إضافتها للحقيبة في الخطوات السابقة.
تمكن العلماء من إيجاد الحل الأمثل لعدد كبير من المشاكل باستخدام الخوارزميات الجشعة ومن أشهر أمثلة هذه الخوارزميات:
* خوارزمية دايكسترا لإيجاد الطريق الأقصر في الرسم، التي ابتكرها العالم الهولندي أيدسكر فيبِ دايكسترا في عام ١٩٥٦م
* خوارزمية دايكسترا لإيجاد الطريق الأقصر في الرسم، التي ابتكرها العالم الهولندي أيدسكر فيبِ دايكسترا في عام ١٩٥٦م
* خوارزمية كروسكال لإيجاد الرسم الشجرية ذات التكلفة الأقل، التي ابتكرها العالم الأمريكي جوزيف كروسكال عام ١٩٥٦م
* خوارزمية هفمان لضغط البيانات، التي ابتكرها العالم الأمريكي ديفيد هفمان عام ١٩٥٢م
vimeo.com
vimeo.com
وتجدر الإشارة إلى أن الخوارزميات الجشعة لا تستطيع إيجاد الحل الأمثل لبعض أنواع مشاكل التحسين، وإنما تنتج حلول مقاربة للحل المثالي. ومن أمثلة هذه المشاكل:
* مشكلة البائع المتجول: وتهدف إلى إيجاد أقصر مسار لزيارة جميع المدن مرة واحدة والعودة إلى نقطة البداية
* مشكلة البائع المتجول: وتهدف إلى إيجاد أقصر مسار لزيارة جميع المدن مرة واحدة والعودة إلى نقطة البداية
* مشكلة تلوين الرسم: وتهدف إلى تلوين رؤوس الرسم بأقل عدد ممكن من الألوان بحيث لا يكون هناك رأسان متجاوران لهما نفس اللون.
* مشكلة الحقيبة: تتعامل هذه المشكلة مع مجموعة من العناصر لكل منها وزن وقيمة، ويجب اختيار مجموعة من العناصر بحيث يكون الوزن الإجمالي أقل من أو يساوي حد معين والقيمة الإجمالية
جاري تحميل الاقتراحات...