لماذا يتخذ التيار و الجهد الموجات الجيبية (sine wave)؟
أي موجة تعود إلى نفس القيمة بشكل دوري تسمى موجة متناوبة (periodic wave). كالموجة المثلثة و المربعة، إلخ يعتبرون موجات متناوبة.
ولكن لماذا التمسك بالموجة الجيبية فقط؟
الموجة الجيبية تحتفظ بطبيعتها الأساسية هذا يعني أن
يتبع
أي موجة تعود إلى نفس القيمة بشكل دوري تسمى موجة متناوبة (periodic wave). كالموجة المثلثة و المربعة، إلخ يعتبرون موجات متناوبة.
ولكن لماذا التمسك بالموجة الجيبية فقط؟
الموجة الجيبية تحتفظ بطبيعتها الأساسية هذا يعني أن
يتبع
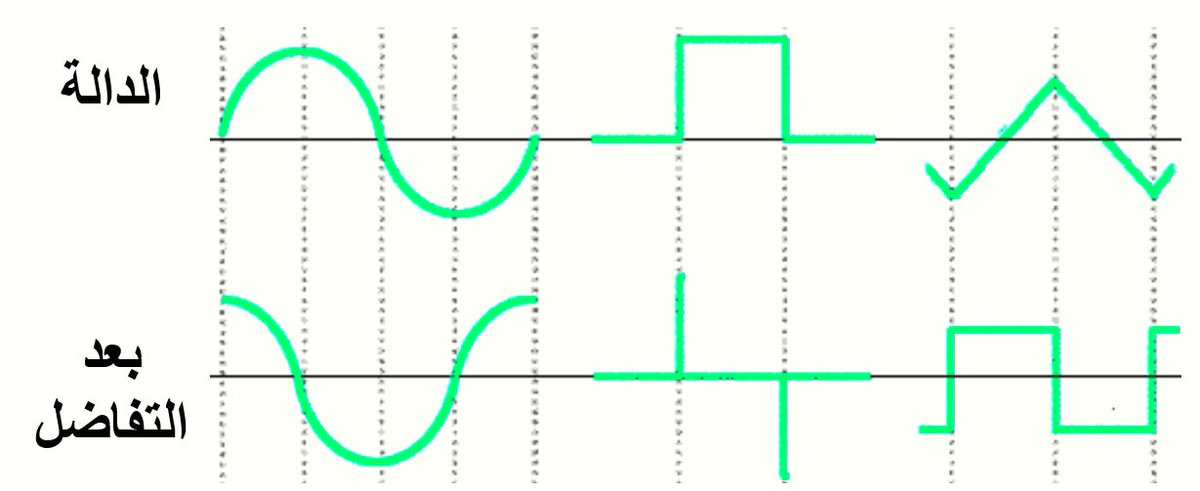
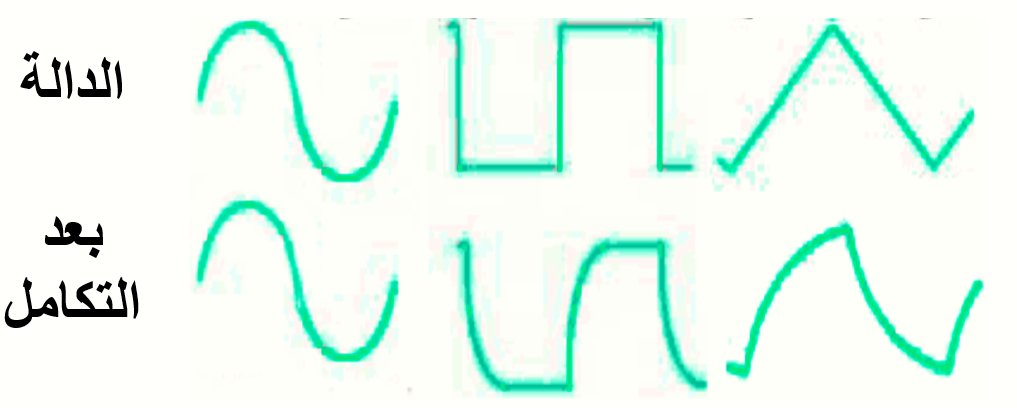تفاضلها (differentiation) أو تكاملها (integration) لهما نفس الطبيعة “sin” تفاضلها و تكاملها “cos” والذي يمكن تمثيله
sin θ = cos (θ - π/2)
أنظر الصورتين لترى كيف تتغير الموجات الأخرى عند تفاضله و تكاملها
ولماذا يهمنا تفاضل و تكامل الموجات؟
للعديد من الأنظمة الكهربائية محاثات
يتبع
sin θ = cos (θ - π/2)
أنظر الصورتين لترى كيف تتغير الموجات الأخرى عند تفاضله و تكاملها
ولماذا يهمنا تفاضل و تكامل الموجات؟
للعديد من الأنظمة الكهربائية محاثات
يتبع
وسعات ومعادلتيهما:
I=C*dV/dt (capacitor), V=L*dI/dt (inductor)
الدوائر المكافئة لخطوط النقل و المحولات و المولدات و المحركات عبارة مجموعة محثات و مكثفات على التوالي و التوازي.
عند العمل مع “sin/cos” يمكن تحليل أنظمة (system analysis) معقدة تتضمن تكاملات ومشتقات مختلطة
يتبع
I=C*dV/dt (capacitor), V=L*dI/dt (inductor)
الدوائر المكافئة لخطوط النقل و المحولات و المولدات و المحركات عبارة مجموعة محثات و مكثفات على التوالي و التوازي.
عند العمل مع “sin/cos” يمكن تحليل أنظمة (system analysis) معقدة تتضمن تكاملات ومشتقات مختلطة
يتبع
(عشرات المكثفات ، المحاثات) بسهولة نسبية. ولكن سيكون من المستحيل تقريبًا حل الموجات الأخرى.
مثلا إذا تم إرسال موجة مثلثة خلال محولين (جهد المحول الثانوي هو مشتقة جهده الأساسي) فسيكون جهد الحمل عبارة عن شكل موجة نبضة!!!
مثلا إذا تم إرسال موجة مثلثة خلال محولين (جهد المحول الثانوي هو مشتقة جهده الأساسي) فسيكون جهد الحمل عبارة عن شكل موجة نبضة!!!
ولكن في حالة “sin/cos” فقط هناك تغيير في ارتفاع الموجة وزاوية الطور (phase angle).
وهناك سبب آخر التوليد فمن السهل توليد الموجة الجيبية.
وهناك سبب آخر التوليد فمن السهل توليد الموجة الجيبية.
جاري تحميل الاقتراحات...