#خوارزميون
@PrograminLovers
أهم أنواع المشكلات في علم الخوارزميات
في هذه السلسلة أستعرض بشكل مختصر أهم أنواع المشكلات التي يتم دراستها في علم الخوارزميات:
١-الترتيب (Sorting)
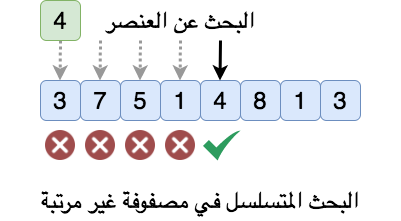
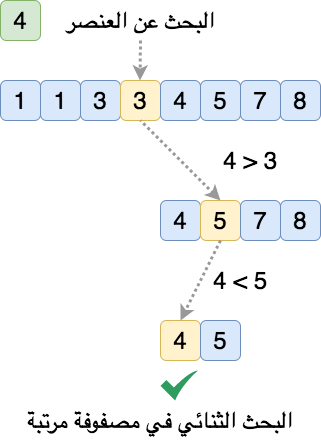
٢-البحث (Searching)
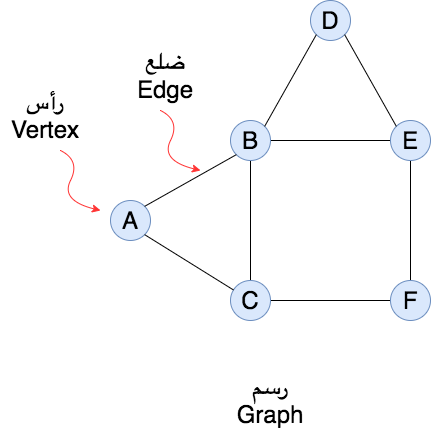
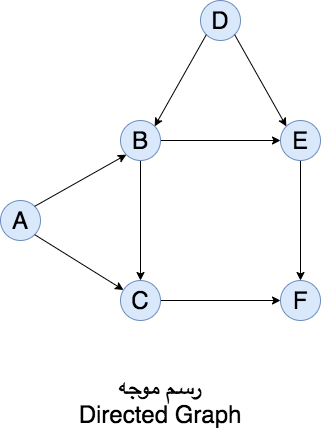
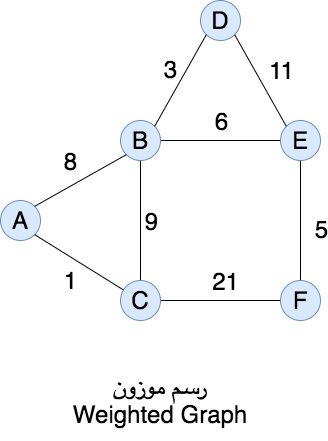
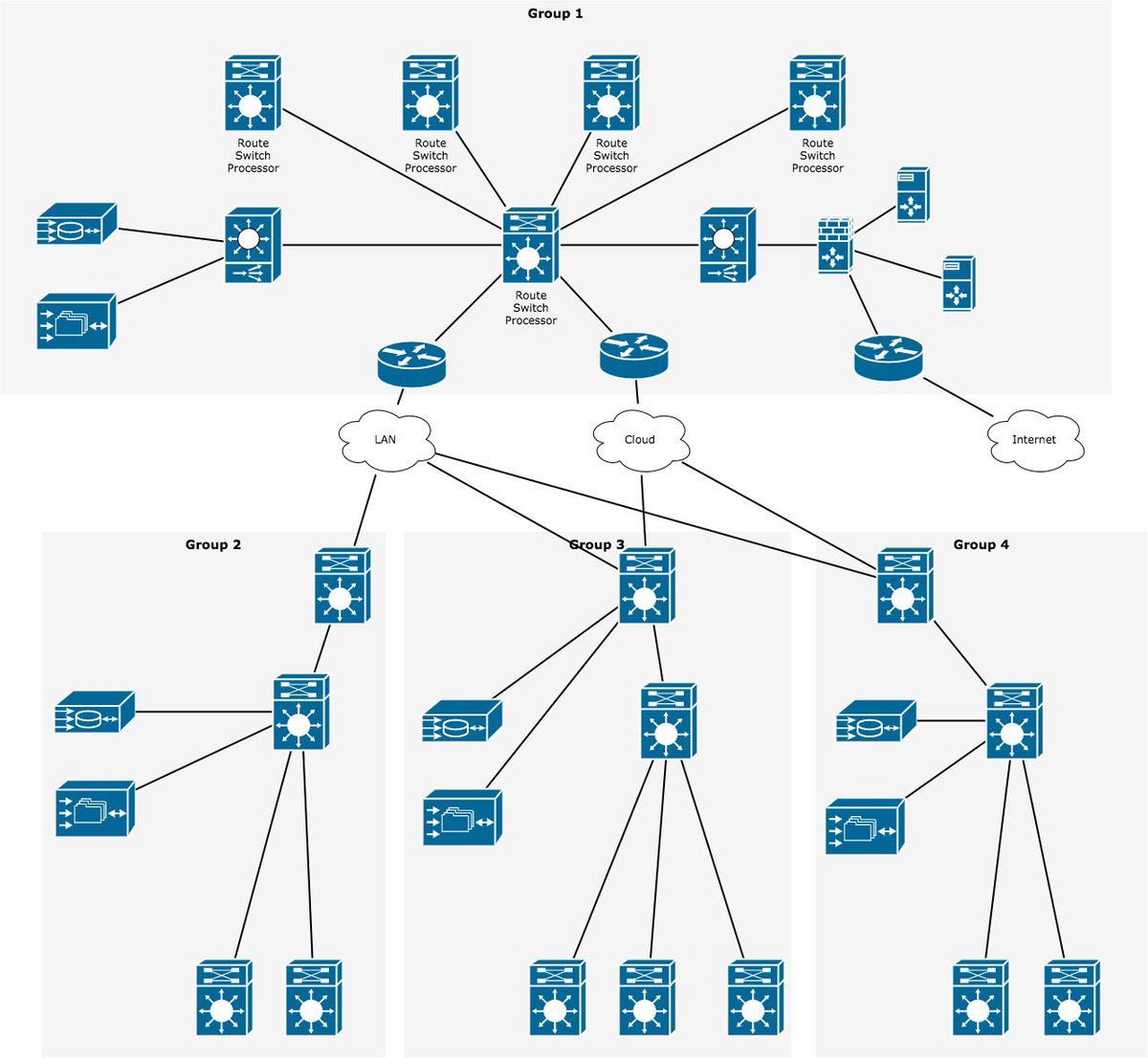
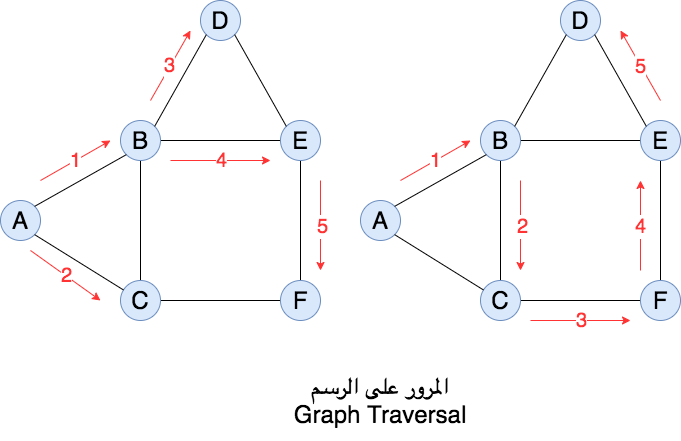
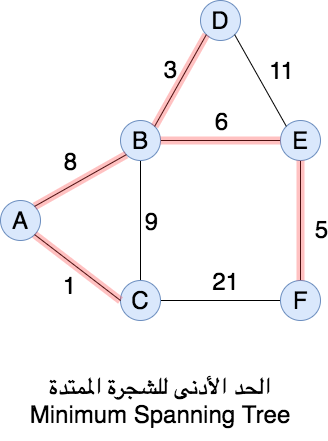
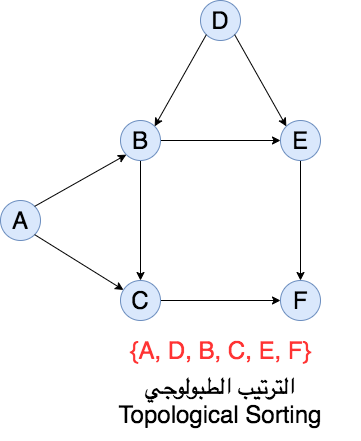
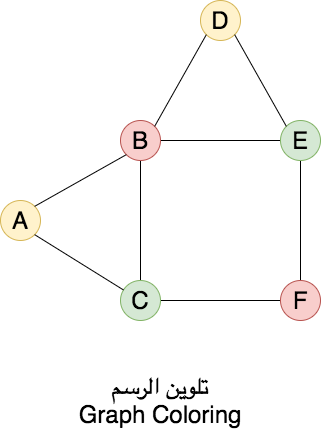
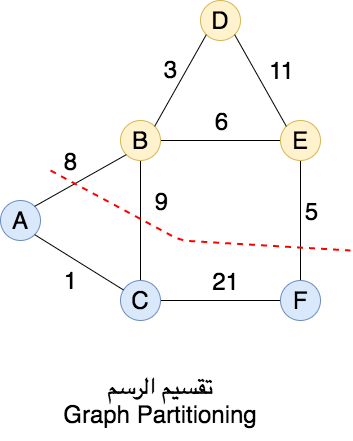
٣-الرسومات (Graphs)
٤- التجميعية (Combinatorial)
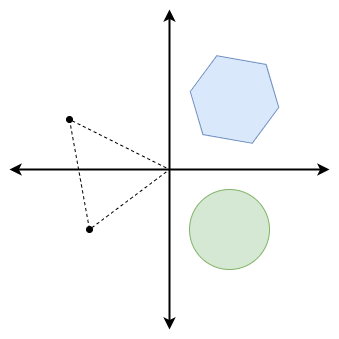
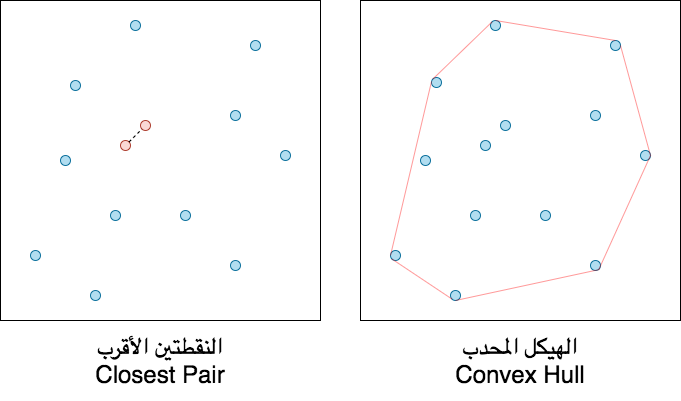
٥- الهندسية (Geometric)
@PrograminLovers
أهم أنواع المشكلات في علم الخوارزميات
في هذه السلسلة أستعرض بشكل مختصر أهم أنواع المشكلات التي يتم دراستها في علم الخوارزميات:
١-الترتيب (Sorting)
٢-البحث (Searching)
٣-الرسومات (Graphs)
٤- التجميعية (Combinatorial)
٥- الهندسية (Geometric)
مشكلة الترتيب (Sorting)
تتمثل هذه المشكلة في إعادة ترتيب عناصر قائمة تصاعديا أو تنازليا. ويوجد نوعين من الخوارزميات التي تتعامل مع هذه المشكلة. الأول (in-place) يرتب عناصر القائمة بدون الحاجة إلى إنشاء قائمة جديدة، والثاني (out of place) يحتاج إلى نسخ العناصر إلى قائمة جديدة
تتمثل هذه المشكلة في إعادة ترتيب عناصر قائمة تصاعديا أو تنازليا. ويوجد نوعين من الخوارزميات التي تتعامل مع هذه المشكلة. الأول (in-place) يرتب عناصر القائمة بدون الحاجة إلى إنشاء قائمة جديدة، والثاني (out of place) يحتاج إلى نسخ العناصر إلى قائمة جديدة
مشكلة البحث (Searching)
تتمثل هذه المشكلة في العثور على قيمة معينة داخل مجموعة من العناصر. يمكن أن تكون هذه العناصر مرتبة أو غير مرتبة. ويوجد نوعين من البحث. الأول (الثنائي) يبحث في القوائم المرتبة، والثاني (التسلسلي) يبحث في القوائم غير المرتبة.
تتمثل هذه المشكلة في العثور على قيمة معينة داخل مجموعة من العناصر. يمكن أن تكون هذه العناصر مرتبة أو غير مرتبة. ويوجد نوعين من البحث. الأول (الثنائي) يبحث في القوائم المرتبة، والثاني (التسلسلي) يبحث في القوائم غير المرتبة.
مشكلة الرسومات (Graph Problems)
يقصد بالرسم هنا مجموعة من النقاط (رؤوس)، يربط بينها خطوط (أضلاع). يمكن أن يكون الرسم موجها بحيث يكون هنا سهم يحدد اتجاه الضلع من نقطة إلى أخرى، أو يكون غير موجه، كما يمكن أن تكون الأضلاع موزونة بحيث يكون لكل ضلع قيمة، أو تكون غير موزونة
يقصد بالرسم هنا مجموعة من النقاط (رؤوس)، يربط بينها خطوط (أضلاع). يمكن أن يكون الرسم موجها بحيث يكون هنا سهم يحدد اتجاه الضلع من نقطة إلى أخرى، أو يكون غير موجه، كما يمكن أن تكون الأضلاع موزونة بحيث يكون لكل ضلع قيمة، أو تكون غير موزونة
وتستخدم الرسوم لتمثيل مجموعة متنوعة من التطبيقات، مثل شبكات النقل، والاتصالات، والحاسب، والانترنت، والشبكات الاجتماعية وجدولة المشاريع، والألعاب.
من أشهر المشكلات:
* المرور: كيفية الوصول إلى جميع النقاط في الرسم
* الحد الأدنى للشجرة الممتدة: مجموعة من الأضلاع الموزونة التي تربط جميع رؤوس الرسم، بدون أي دورات وبأقل وزن للأضلاع.
* الترتيب الطوبولوجي: ترتيب الرؤوس بحيث لكل ضلع موجه من أ إلى ب، يأتي أ قبل ب في الترتيب
* المرور: كيفية الوصول إلى جميع النقاط في الرسم
* الحد الأدنى للشجرة الممتدة: مجموعة من الأضلاع الموزونة التي تربط جميع رؤوس الرسم، بدون أي دورات وبأقل وزن للأضلاع.
* الترتيب الطوبولوجي: ترتيب الرؤوس بحيث لكل ضلع موجه من أ إلى ب، يأتي أ قبل ب في الترتيب
بعض مشاكل الرسومات صعبة جدا، وتتطلب استخدام خوارزميات مقاربة ومن أشهرها:
* تلوين الرسم: تلوين الرؤوس بأقل عدد ممكن من الألوان بحيث لا يكون هناك رأسان متجاوران لهما نفس اللون.
* تقسيم الرسم: التقسيم إلى مجموعتين متساويتين بحيث يكون مجموع أوزان الأضلاع التي يتم فصلها أقل ما يمكن
* تلوين الرسم: تلوين الرؤوس بأقل عدد ممكن من الألوان بحيث لا يكون هناك رأسان متجاوران لهما نفس اللون.
* تقسيم الرسم: التقسيم إلى مجموعتين متساويتين بحيث يكون مجموع أوزان الأضلاع التي يتم فصلها أقل ما يمكن
المشاكل التجميعية أو الاندماجية (Combinatorial Problems)
تتمثل هذه المشكلة في إيجاد تجميع أو ترتيب أو تخصيص مجموعة من العناصر التي تفي بشروط معينة.
تتمثل هذه المشكلة في إيجاد تجميع أو ترتيب أو تخصيص مجموعة من العناصر التي تفي بشروط معينة.
ومن أمثلة هذه المشاكل التجميعية:
* مشكلة البائع المتجول: وتهدف إلى إيجاد أقصر مسار لزيارة مجموعة من المدن مرة واحدة والعودة إلى نقطة البداية
analyticsvidhya.com
* مشكلة البائع المتجول: وتهدف إلى إيجاد أقصر مسار لزيارة مجموعة من المدن مرة واحدة والعودة إلى نقطة البداية
analyticsvidhya.com
تعد المشكلات الاندماجية هي أصعب المشكلات في علم الحاسب من الناحيتين النظرية والعملية. وتكمن صعوبة هذه المشاكل في ناحيتين:
١- عدد احتمالات حل المشكلة يتزايد بسرعة مع زيادة حجم المشكلة، ويصل إلى حد لا يمكن إيجاد الحل الأمثل لها في زمن معقول حتى بالنسبة لمشكلة متوسطة الحجم
١- عدد احتمالات حل المشكلة يتزايد بسرعة مع زيادة حجم المشكلة، ويصل إلى حد لا يمكن إيجاد الحل الأمثل لها في زمن معقول حتى بالنسبة لمشكلة متوسطة الحجم
على سبيل المثال هناك أكثر من ٦ مليار احتمال لترتيب ١٣ مدينة في مشكلة البائع المتجول
٢- لا توجد خوارزميات لحل معظم هذه المشكلات في فترة زمنية مقبولة. علاوة على ذلك يعتقد معظم علماء الحاسب أن مثل هذه الخوارزميات غير موجودة. وحتى الآن لم يتمكن أي أحد من إثبات هذا الافتراض أو نفيه
٢- لا توجد خوارزميات لحل معظم هذه المشكلات في فترة زمنية مقبولة. علاوة على ذلك يعتقد معظم علماء الحاسب أن مثل هذه الخوارزميات غير موجودة. وحتى الآن لم يتمكن أي أحد من إثبات هذا الافتراض أو نفيه
المشاكل الهندسية (Geometric Problems)
تتعامل هذه المشاكل مع العناصر الهندسية مثل النقاط والخطوط والمضلعات. تدخل هذه المشاكل في العديد من التطبيقات الحديثة مثل رسومات الحاسب، والروبوتات، والتصوير المقطعي.
تتعامل هذه المشاكل مع العناصر الهندسية مثل النقاط والخطوط والمضلعات. تدخل هذه المشاكل في العديد من التطبيقات الحديثة مثل رسومات الحاسب، والروبوتات، والتصوير المقطعي.
ومن أمثلة هذه المشاكل ما يلي:
* مسألة النقطتين الأقرب (Closest Pairs): عند إعطاء عدد من النقاط في المستوى، المطلوب إيجاد أقرب نقطتين لبعضهما.
* الهيكل المحدب (Convex Hull): تتطلب هذه المشكلة العثور على أصغر مضلع محدب يتضمن جميع نقاط مجموعة معينة.
* مسألة النقطتين الأقرب (Closest Pairs): عند إعطاء عدد من النقاط في المستوى، المطلوب إيجاد أقرب نقطتين لبعضهما.
* الهيكل المحدب (Convex Hull): تتطلب هذه المشكلة العثور على أصغر مضلع محدب يتضمن جميع نقاط مجموعة معينة.
جاري تحميل الاقتراحات...