"سلسلة تغريدات في علم التحكم control theory "
قمت بتثبيث سرعة سيارتي على 110كم/س ، لكن مع نزول في نفق او اعتلاء في جسر فإني ألاحظ تغيرا بسيطا في السرعة تتلافاه السيارة بعد لحظات بتسارع لأعلى أو لأسفل. فلم حدث هذا و هل يدل هذا على سوء برمجة للمثبت؟
#هندسة_كهربائية
قمت بتثبيث سرعة سيارتي على 110كم/س ، لكن مع نزول في نفق او اعتلاء في جسر فإني ألاحظ تغيرا بسيطا في السرعة تتلافاه السيارة بعد لحظات بتسارع لأعلى أو لأسفل. فلم حدث هذا و هل يدل هذا على سوء برمجة للمثبت؟
#هندسة_كهربائية
و حتى نفهم الأمر من الأساس، شاهد تمثيل النظام بالصورة.
P(s) تشير إلى محرك السيارة، C(s) المتحكم بالسرعة أو المثبت،،، من أقصى اليمين y هي السرعة الحقيقية للسيارة، و من أقصى اليسار r(t) السرعة المطلوب الثبات عندها.
P(s) تشير إلى محرك السيارة، C(s) المتحكم بالسرعة أو المثبت،،، من أقصى اليمين y هي السرعة الحقيقية للسيارة، و من أقصى اليسار r(t) السرعة المطلوب الثبات عندها.
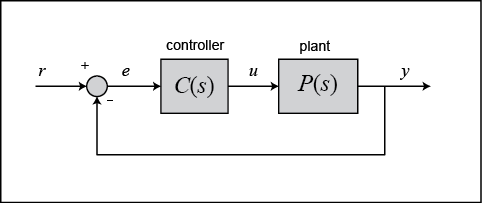
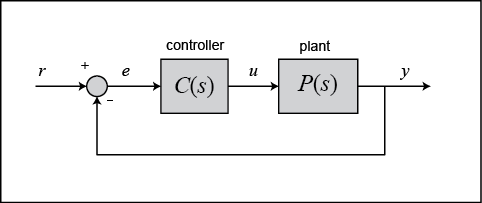
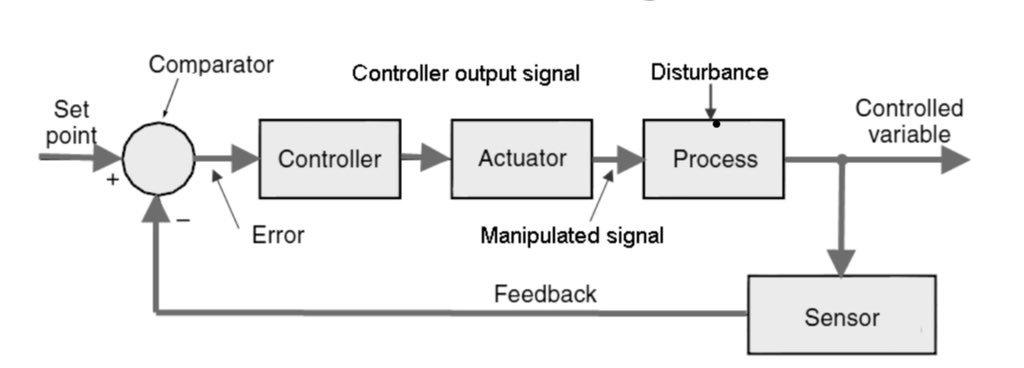
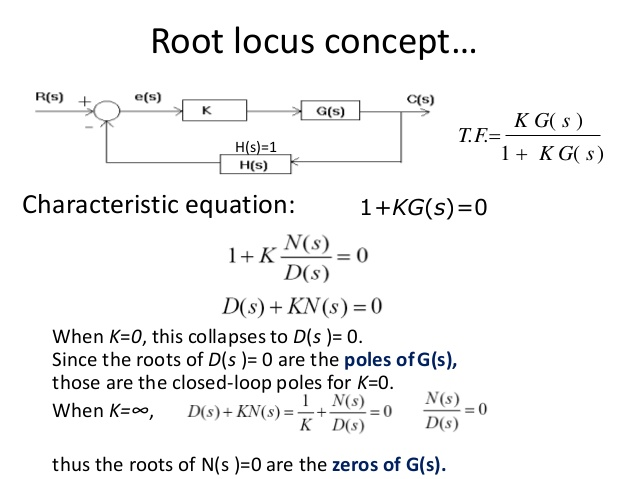
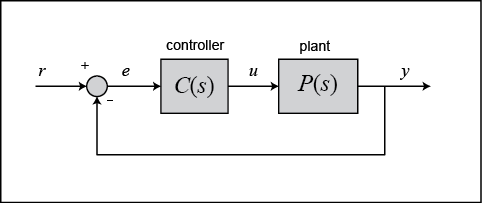
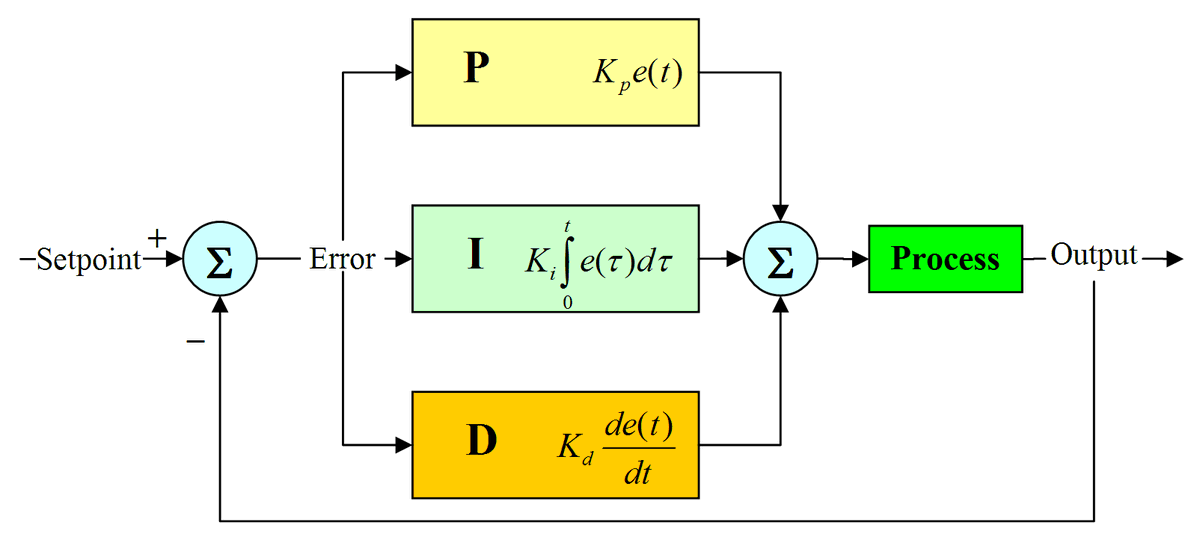
من النظر إلى الصورة نلاحظ وجود خط رجعة من y يسمى الأثر الرجعي feedback، يطرح من القيمة المطلوبة r(t) و تكون النتيجة دالة تسمى دالة الخطأ e(t) تدخل على مثبت السرعة، و عليها يعطي أوامره للمحرك بزيادة العمل أو بالتوقف، و قد يكون النظام مرتبطًا بالمكابح للتحكم الشامل بالمركبة.
هناك أنواع عديدة من المتحكمات controller التي تستخدم بالتطبيقات، أشهرها و أبسطها On - off controller ،فإن كانت السرعة أعلى من المطلوب أمر المحرك بتخفيف العمل، و إن كانت أقل، أمره بالعمل أكثر وهكذا.
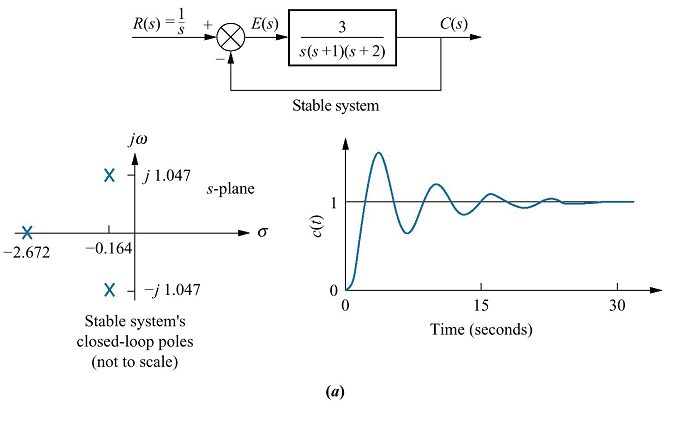
لكن هذا لا يفسر الذبذبة بشكل في السرعة في الأحوال التي ذكرنا، فنعيد السؤال مجددا!
لكن هذا لا يفسر الذبذبة بشكل في السرعة في الأحوال التي ذكرنا، فنعيد السؤال مجددا!
في علم التحكم لدينا ما نسميه differential gap و هي نسبة معينة من القيمة المطلوبة أستطيع التغاضي عنها بزمن معين، فمثلا في حالتنا سأسمح لسرعة السيارة أن تصل 114كم/س في ثواني و سأعيدها لاحقا، ولا حاجة حقيقية للتدقيق المستمر لأن لا تتغير السرعة أبدا عن 110 فالهامش مقبول و مهم أيضًا!
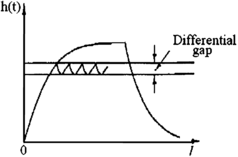
تكمن أهمية هذا الهامش بأنه يعطي نفسا للمتحكم،فتخيل أننا سنفرض عليه العمل إن بلغت السرعة 109.9أو 110.1كم/س ، نظريا هذا ممكن لكن سيكون مكلفا على المُصنع،ويقلل من العمر الافتراضي للمتحكم و للمحرك أيضا!
نأخذ مثالا آخر، تخيل أن لدينا متحكما في خزان و مضخة على أن نسبة المياه ستكون 90%
نأخذ مثالا آخر، تخيل أن لدينا متحكما في خزان و مضخة على أن نسبة المياه ستكون 90%
تخيل أنه لما انتهى الخزان من التعبئة عند النسبة المطلوبة، نقصت قليلا إلى 89.9% فعملت المضحة، أو بلغت نسبة 90.1% ففتح الخزان قنواته أو رن جرس الإنذار! لو تخيلنا الأمر، سيصاب المتحكم بالهلع و ستتعطل الآلات عاجلا أم آجلا. و أولا و أخيرا لم يكن التطبيق يحتاج هذه الدقة المتناهية!!
لذلك في علم التحكم وإن جئنا لتصميم متحكمات مختلفة، فإننا نصممها بناءً على الاحتياجات المطلوبة ولا نزيد ،فالتطبيقات التي ذكرنا لا تحتاج دقة متناهية لأسباب تتعلق بالجودة و طول عمر المنتج، لكن إن صممنا متحكمات في مفاعلات نووية تتحكم مثلا بعدد النيوترونات المتطايرة فهنا الدقة مطلوبة
من التطبيقات التي لن تحتاج إلى دقة متناهية مثل: حساس لدرجة حرارة الغرفة.
فلا بأس إن ضبطها المستخدم على 23 درجة مئوية، و سمحت لها هامشًا بالارتفاع إلى 23.9 مثلا.
و هكذا دواليك مع كثير من التطبيقات المختلفة.
فلا بأس إن ضبطها المستخدم على 23 درجة مئوية، و سمحت لها هامشًا بالارتفاع إلى 23.9 مثلا.
و هكذا دواليك مع كثير من التطبيقات المختلفة.
يأتي الاستغراب من بعض القراء أو الذين يتعلمون هذه المادة مادة التحكم، كيف يمكن أن نمثل نظام سرعة السيارة مثلا على أنها y ، و المدخلات على النظام و غيرها بهذا الشكل؟
أين أجهزة الطاقة؟ و السرعة كيف قيست و أصبحت تمثل بإشارة كهربائية؟ و كيف تتحكم إشارة كهربائية بمحرك السيارة؟
أين أجهزة الطاقة؟ و السرعة كيف قيست و أصبحت تمثل بإشارة كهربائية؟ و كيف تتحكم إشارة كهربائية بمحرك السيارة؟
لدينا في الهندسة الكهربائية جهازان يسميان : sensor و actuator، الأول يستشعر وحدة ميكانيكية و يحولها إلى إشارة كهربائية، و الثاني بالعكس. لكن بالعادة و لأجل معرفتنا المسبقة لذلك نمثل النظام بدون وضعهما؛ فذلك أمر بديهي. و أحيانا نضعها كما بالصورة:
2)
تعد الخطوة الأولى لمحاكاة أي نموذج على أرض الواقع هي وصفه بمعادلات رياضية استنادًا إلى العلوم الأساسية الفيزياء و الكيمياء و الأحياء. لما نوجد علاقة TF و هي تساوي المخرجات على المدخلات،، لاحظ G(s) في الصورة التالية هي الـTF المقصودة.
تعد الخطوة الأولى لمحاكاة أي نموذج على أرض الواقع هي وصفه بمعادلات رياضية استنادًا إلى العلوم الأساسية الفيزياء و الكيمياء و الأحياء. لما نوجد علاقة TF و هي تساوي المخرجات على المدخلات،، لاحظ G(s) في الصورة التالية هي الـTF المقصودة.
و لأن الكمبيوتر لا يمكنه التعامل مع معادلات بهذا الشكل، فيجب علينا ترجمتها إلى شكل معادلة مكتوبة على شكل مصفوفة كما بالسؤال الثاني بالصورة السابقة و هناك طريقة رياضية تقليدية، و الأنجع من ذلك استخدام دالة في برنامج MATLAB تُدعى : " tf2ss " تفي بالغرض.
الكتابان بالصورة يزخران بعديد الأمثلة على ما ذكرنا من أنظمة تم تمثيلها على معادلات مثل ما تحدثنا سابقا. الجدير بالذكر أن لا نظام واقعي يمكن تمثيله بشكل تام على شكل معادلات خطية، لأن واقع التجربة مخالف بنسبة معينة، و بشكل عام العلاقة الخطية الكاملة غير كاملة في كثير من الأحيان..
لذلك هناك علم فرعي في التحكم و له مواد تدرس بالدراسات العليا أكاديميا في تمثيل الأنظمة غير الخطية بمعادلات خطية تحت شروط و فترات معينة على محور x. كل هذا حتى نستطيع وصفها بالرياضيات و إدخالها للحاسوب..
Root loucus:
طريقة رياضية هندسية توضح بالرسم سلوك أقطاب النظام مع التغير في بسطه K، و الهدف منها في الأخير التنبؤ بسلوكيات النظام، فمع صعودنا برسم (روت لوكس) فإن الذبذبة صعودا و نزولا تزيد، و مع اتجاهنا لليسار فإن النظام يستقر أسرع و تقل الذبذبة لكن مع صعود أعلى في النطة الأولى.
طريقة رياضية هندسية توضح بالرسم سلوك أقطاب النظام مع التغير في بسطه K، و الهدف منها في الأخير التنبؤ بسلوكيات النظام، فمع صعودنا برسم (روت لوكس) فإن الذبذبة صعودا و نزولا تزيد، و مع اتجاهنا لليسار فإن النظام يستقر أسرع و تقل الذبذبة لكن مع صعود أعلى في النطة الأولى.
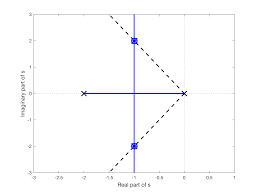
و مع ذهابنا إلى اليمين فإن النظام يقترب إلى حالة عدم الاستقرار و الثبات unstable، و مع وصوله إلى منحنى y فإنه يكون في نقطة حرجة، و إن انتقل إلى اليمين فإن النظام بالكلية unstable غير صالح لأن ينفذ. طريقة تمثيل رسمة (ر.لوكس)بسيطة، لكن هناك أمر في MATLAB يختصر هذا كله و يرسم النظام
صفحة هذا الدرس في وكيبيديا واضحة:
en.wikipedia.org
و هنا بعض الزملاء يشرحون كيفية تمثيلها:
youtube.com
en.wikipedia.org
و هنا بعض الزملاء يشرحون كيفية تمثيلها:
youtube.com
هنا تغريدة عن قنابل Paveway الموجهة ليزريا وكيف سيكون نموذج عملها استنادا على ما قلنا سابقا في علم التحكم.
لما تُسقط القنبلة من الطائرة يكون داخلها كمبيوتر متكامل،و به جهاز GPS لتحديد المواقع، و مستقبل هوائي يستقبل الإحداثية المرسلة إلى القنبلة لمقارنتها.
لما يسقط الصاروخ من الطائرة يبدأ نظام تحديد المواقع في الصاروخ بإرسال الإحداثية كل لحظة إلى الكمبيوتر، فيقارن هل هي ذات النقطة المطلوبة؟ فإن كانت لا، يبتدئ بتحريك الزعانف و يدفع غازات إلى الخلف للإسراع، حتى يصل إلى النقطة المطلوب السقوط عليها.
لاحظ أن الكمبيوتر سيكون بالصورة هو الـ Plant، و الذي سيقرر تحريك الزعانف و دفع الغازات من الخلف هو الـController
y:ستكون المكان الحالي للصاروخ
e:نسبة الخطأ ما بين الإحداثية المطلوبة و الحالية
u:قرار الكنترولر بحسب نسبة الخطأ الواصلة إليه،سيأمر الصاروخ بالتحرك أو البقاء في مكانه؟
y:ستكون المكان الحالي للصاروخ
e:نسبة الخطأ ما بين الإحداثية المطلوبة و الحالية
u:قرار الكنترولر بحسب نسبة الخطأ الواصلة إليه،سيأمر الصاروخ بالتحرك أو البقاء في مكانه؟
إحدى أنواع المتحكمات controllers و أشهرها هو المتحكم PID، و هو اختصار لـ Proportional Integral Derivative controller، أي متحكم تناسبي تكاملي تفاضلي مع قيمة الخطأ الداخلة إليه. لاحظ الصورة المرفقة، للمتحكم ثلاث قيم Kp,Ki,Kd و هي تتحكم بأداء النظام.
في الصور المرفقة أيضا في كل مرة غيرنا قيمًا من الثلاث قيم للمتحكم و بالتالي تغير الأداء للنظام. و لكل واحد منها مزايا و عيوب، من خلال التوفيق بينها نصمم النظام بحسب الاحتياج الخاص لكل تطبيق.
هذا جدول نقلته من ويكبيديا عن القيم الثلاث، و الذي يوضح المزايا و العيوب. في الصورة الأخرى شرح لكل مصطلح، حيث:
زمن الصعود: raise time
النطة: peak value
زمن الاستقرار: settling time
الخطأ عند الاتزان: نسبة الخطأ ما بين النتيجة المطلوبة و الحالية.
زمن الصعود: raise time
النطة: peak value
زمن الاستقرار: settling time
الخطأ عند الاتزان: نسبة الخطأ ما بين النتيجة المطلوبة و الحالية.
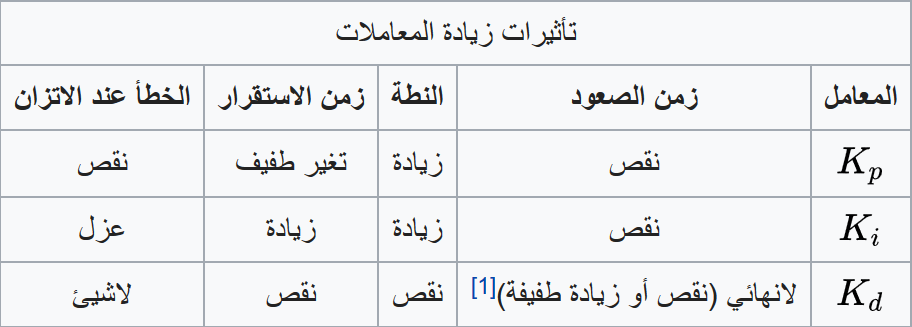
مع العلم أنه بالنسبة لمتحكمات PID فإنه في كثير من التطبيقات يستبعد الجزء التفاضلي D،وذلك لأنه حساس جدا مع الضجيج noise. الأكثر استخداما هو PI.
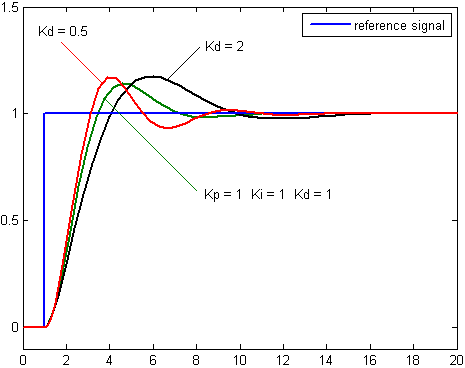
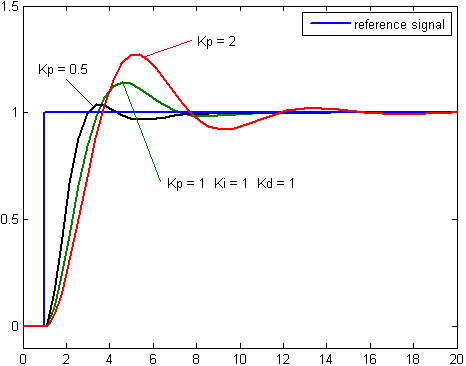
هذا النوع من المتحكمات من الأشهر،وله برامج عديدة لنمذجته على الحاسب كما في برنامج ماتلاب،و ذلك لاختيار القيم الأمثل للنظام المراد تصميمه.
هذا النوع من المتحكمات من الأشهر،وله برامج عديدة لنمذجته على الحاسب كما في برنامج ماتلاب،و ذلك لاختيار القيم الأمثل للنظام المراد تصميمه.
جاري تحميل الاقتراحات...